https://www.bigocheatsheet.com/ https://discrete.gr/complexity/

Complexities

Space complexity

Space complexity is the amount of memory (space) required by the algorithm.

Note that, stack space in the recursive calls counts too. If the calls don't exist simultaneously, it doesn't count.

Nghĩa là đối với đệ quy, chỉ tính khi các biến cùng tồn tại tại 1 thời điểm, chứ không tính tổng cộng.

Time complexity

Time complexity is the concept of asymptotic runtime. It is a parallel concept to the space complexity.

Academics use $big O$, $big θ$ (theta), $big Ω$ (omega) to describe runtime. They are used to describe the efficiency of algorithms

Some common runtimes are $O(log N)$, $O(N log N)$, $O(N)$, $O(N^2)$, $O(2^n)$.

0

$O$ describes an upper bound on the time. O lớn miêu tả một chặn trên cho tốc độ tăng của hàm.

Nếu $f(x) = O(g(x))$ khi $x \rightarrow a$ thì: $\limsup\limits_{x \to a} | \frac{f(x)}{g(x)} | \le \infty$

Ví dụ, xét $x \to +\infty$, ta có:

• Nếu $f(x) = 10, g(x) = 1$ thì $f(x) = O(g(x))$
• Nếu $f(x) = 10x^3, g(x) = x^4$ thì $f(x) = O(g(x))$ nhưng $g(x) \neq O(f(x))$

Ω

$Ω$ is the equivalent concept but for lower bound.

θ

$θ$ means both $O$ and $Ω$, it gives a tight bound on runtime.

Some notes:

• Industry tends to use $big O$ (people seem to have merged $0$ and $θ$ together).
• There is no particular relationship between best/worst/expected case and big O/theta/omega:
• best, worst, expected cases describe the big O (or big theta) time for particular inputs or scenarios.
• whilst, big 0, omega, theta describe the upper, lower, tight bounds for the runtime.

Rules

Drop the constants

$Big O$ describes the rate of increase $\rightarrow$ drop constants at runtime.

E.g.: $O(2N)$ is $O(N)$.

So sánh 2 đoạn code dưới đây:

for (int x : array) {
 if (x < min) min = x;
 if (x > max) max = x;
}

for (int x : array) {
 if (x < min) min = x;
}
for (int x : array) {
 if (x > max) max = x;
}

Thoạt nhìn thì đoạn code 1 chỉ có 1 vòng lặp, tuy nhiên lại có 2 dòng lệnh trong vòng lặp, còn đoạn code 2 thì có 2 vòng lặp nhưng chỉ có 1 dòng lệnh mỗi vòng. Để biết cái nào nhanh hơn, ta cần đi tới mức độ mã máy để xem tổng số câu lệnh thực hiện, hay cách compiler tối ưu cách chạy, cách cấp phát cấu trúc dữ liệu của mỗi máy tính, v.v.

Tuy nhiên, chúng ta không cần phải đi sâu vào phức tạp như vậy. Chỉ cần nhớ rằng, trong 1 số trường hợp, $O(N)$ có thể chạy nhanh hơn $O(1)$ và đôi khi không có nghĩa là cứ $O(N)$ thì sẽ tốt hơn $O(N^2)$.

Nên nhớ rằng, các quy tắc của $O(f(N))$ được tính toán trong điều kiện $N \rightarrow \infty$, cho nên những quy tắc chỉ càng khả thi khi N càng lớn.

Drop the non-dominant terms

Cũng giống như bỏ hằng số, trong biểu thức $f$, ta sẽ bỏ tham số có độ mạnh thấp hơn.

Ví dụ: $O(N^2 + N^2) \rightarrow O(N^2)$ (cũng như $O(2N^2) \rightarrow O(N^2)$).

Một số ví dụ khác:

• $O(N^2 + N) \rightarrow O(N^2)$
• $O(N + logN) \rightarrow O(N)$
• $O(5*2^N + 1000N^{100}) \rightarrow O(2^N)$

Tuy nhiên, quy tắc trên chỉ áp dụng với cùng loại tham số. Ví dụ $O(B^2 + A)$ thì ta không thể bỏ được cái nào vì không có đủ thông tin về $A$ và $B$.

Bảng dưới đánh giá độ mạnh yếu của một số big O thông dụng:

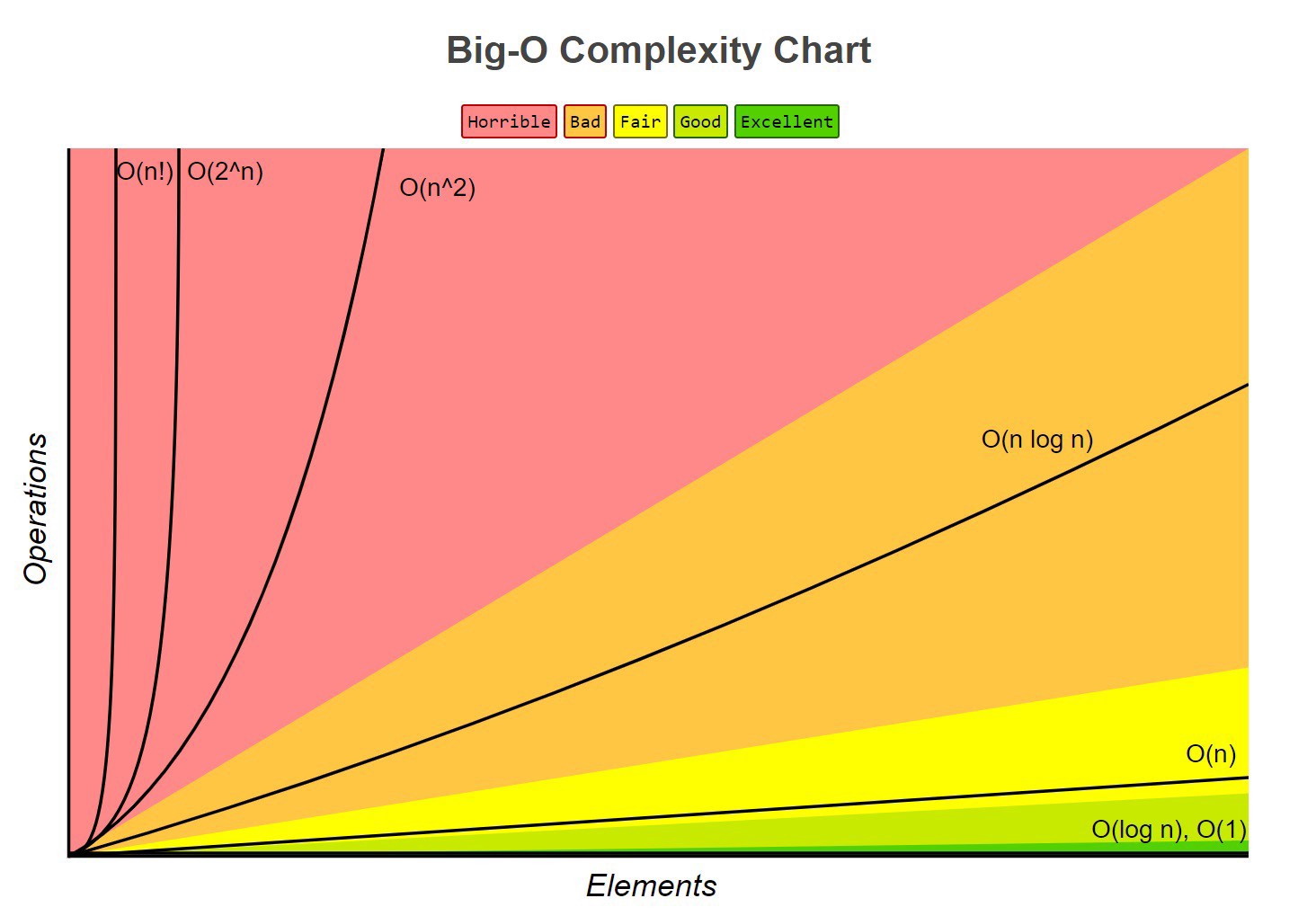
Add & multiply in multi-part algorithms

Khi thuật toán kiểu "làm việc này xong rồi mới làm việc khác" $\to$ xài phép cộng.

for (int a : arrA) {
  print(a);
}
for (int b : arrA) {
  print(b);
}

O(A + B)

Khi thuật toán kiểu "làm cái này mỗi lần mày làm cái kia" $\to$ xài phép nhân.

for (int a: arrA) {
  for (int b: arrB) {
    print(a, b);
  }
}

O(A*B)

Amortized Time

Ví dụ với mảng động. Ban đầu mảng động sẽ cấp phát cho ta một vùng nhớ N để sử dụng, nếu ta sử dụng quá vùng nhớ đó, mảng sẽ tự giãn ra với kích thước gấp đôi 2N, sau đó nó sẽ sao chép N phần tử cũ qua mảng mới. Việc thêm phần tử vào sẽ tốn O(N).

Tuy nhiên, việc sử dụng hết bộ nhớ được cung cấp cũng hiếm khi xảy ra, vì vậy hầu như việc thêm phần tử chỉ tốn O(1).

Ví dụ trên là ví dụ về thời gian khấu hao.

Amortized time is the way to express the time complexity when an algorithm has the very bad time complexity only once in a while besides the time complexity that happens most of time.

Với trường hợp trên thời gian khấu hao là gì? Khi chèn phần tử mảng, chúng ta gấp đôi kích thước mảng. Vậy sau X phần tử, chúng ta gấp đôi kích thước từ 1, 2, 4, 8, 16, ..., X. Vậy tổng cộng tốn 1 + 2 + 4 + 8 + 16 + ... + X = 2X.

Như vậy, chèn phần tử sẽ tốn O(2X). Thời gian khấu hao cho mỗi lần chèn là O(1).

Runtime patterns

Log N

Khi thuật toán có số lượng phần tử bị giảm một nửa mỗi lần, thời gian chạy thường sẽ là $O(\log N)$

Ví dụ điển hình là tìm kiếm nhị phân.

Recursive

Khi có đệ quy mà gọi nhiều hàm, thời gian chạy thường sẽ là $O(2^N)$, hay còn là $O(branches^depth)$. Ví dụ:

int f(int n) {
  if (n <= 1) {
    return 1;
  }
  return f(n - 1) + f(n - 1);
}

> runtime: O(2^N)